Cómo Sacar Desviación Estándar En Excel
¿Quieres saber cómo sacar desviación estándar en Excel? La desviación estándar en Excel era una función incorporada en Excel para 2007 y versiones anteriores que se utilizó para obtener la desviación estándar en función de una muestra dada como argumento, pero en las versiones de Excel 2010 y superiores tenemos otras fórmulas para calcular la desviación estándar que es STDEV. P y STDEV.S.
En este tutorial te enseñaremos cómo realizarlo siguiendo simples pasos. No tendrás que hacer cursos extensos para esto (aunque no es malo tener un certificado) sin más preámbulos, veamos como es el procedimiento:
También te puede interesar: Cómo Ocultar Celdas En Excel
¿Cómo sacar desviación estándar en Excel?
Este método es muy sencillo. Por ejemplo: supón que tienes los puntos de datos 5, 3, 6, 8 y 10.
- Puntos de datos totales: 5
- Suma de puntos de datos: 32
- Promedio (Media) = 32/5 = 6.4
- Desviación estándar Excel = 2.7
Esto significa que la mayoría del rango de puntos de datos está dentro de 2.7 del valor promedio, es decir, entre 3.7 y 9.1 (a ambos lados del valor promedio de 6.4).
- Si el valor de la desviación estándar es menor, entonces la frecuencia de los puntos de datos está más cerca del valor medio (promedio).
- Si el valor de la desviación estándar es más alto, entonces la frecuencia de los puntos de datos es más amplia que el valor medio (promedio).
Calcular la desviación estándar en Excel
Cuando tratamos con datos cuantitativos, siempre buscamos un elemento típico del conjunto de datos. ¿Cuál es el medio del punto de datos? es decir, el valor medio o la media de los puntos de datos.
La desviación estándar nos ayuda a comprender qué tan dispersos están los datos. Especialmente en la industria financiera, los datos de precios se utilizan como medida de volatilidad.
Los siguientes ejemplos nos permitirán comprender prácticamente el concepto de Excel de desviación estándar.
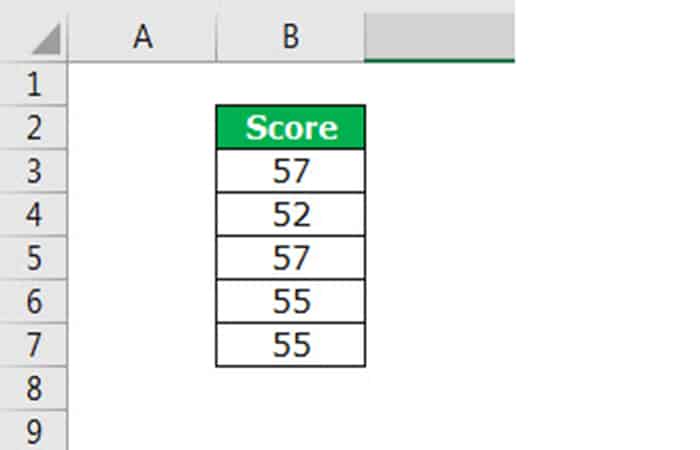
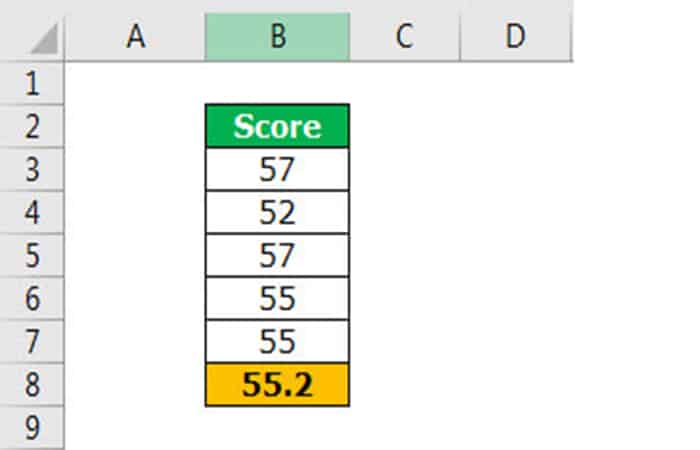
A continuación se muestran los puntajes del nivel de habilidad de los empleados en una empresa. A partir de este conjunto de datos, necesitamos calcular el valor de la desviación estándar.
Sigue los pasos a continuación para calcular la desviación estándar en Excel.
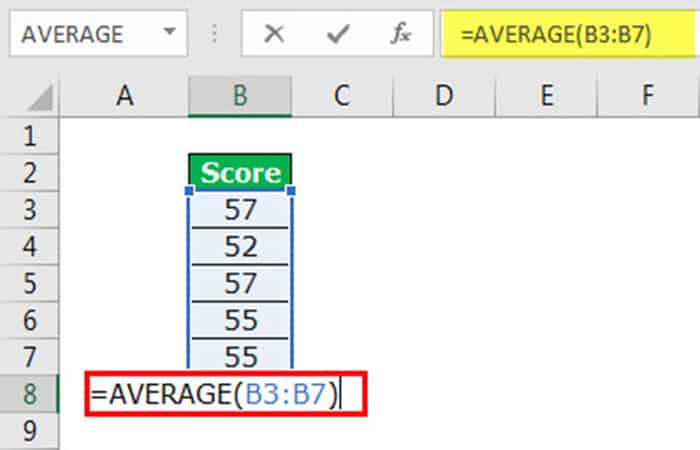
- Paso 1: Calcula la media (promedio) de los datos en Excel.
Media = 55,2
Por tanto, el valor medio de los datos es 55,2, es decir, la puntuación media del nivel de habilidad de los empleados es 55,2
- Paso 2: Calcula la diferencia de puntuación de cada empleado con respecto al valor medio y encuentre la diferencia.
Varianza =
Varianza =
Varianza = 3.36
- Paso 3: Calcular SD (Desviación estándar de Excel)
SD es solo la raíz cuadrada de la varianza.
DE = 1,83
Conclusión: Entonces, la historia de este cálculo es que el rango de puntaje de los empleados va desde 53.37 a 57.03.
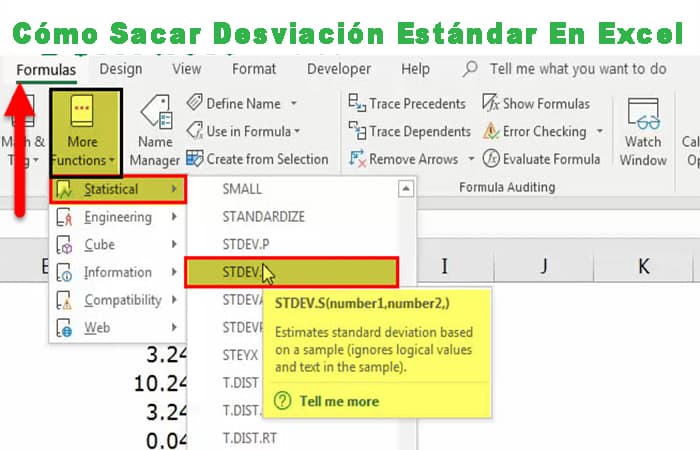
Fórmulas de desviación estándar en Excel
En Excel, tenemos un total de 8 tipos de fórmulas de desviación estándar en Excel.
Estas 8 fórmulas se encuentran en dos grupos: Muestra y población.
STDEV.S, STDEVA, STDEV, DSTDEV está en Sample.
STDEV.P, STDEVP, STDEVPA, DSTDEVP está en Población.
- Población significa que está considerando el conjunto de datos completo.
- Muestra significa que es muy difícil usar todos los datos y solo está tomando la muestra del conjunto de datos.
Podemos usar datos de muestra de todo el conjunto de datos para calcular la desviación estándar y hacer inferencias para todo el conjunto de datos.
- En casi todos los casos, utilizamos la fórmula STDEV.S para calcular la desviación estándar en Excel. Esto se usa cuando queremos usar solo los valores numéricos e ignorar los valores de texto.
- Si deseas utilizar valores de texto en el rango, utiliza STDEVA. Toma texto y valor FALSO como 0 y VERDADERO como 1.
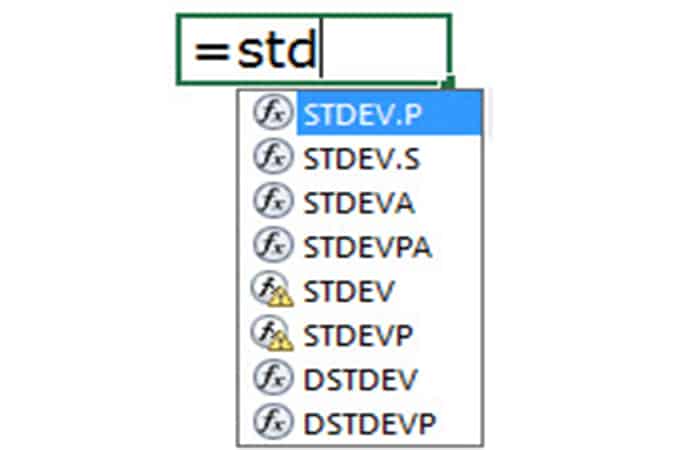
Cómo sacar desviación estándar en Excel usando la fórmula STDEV.S
La fórmula de STDEV.S en Excel incluye solo números.
- Número 1: el primer valor de la muestra de toda la población. Puedes seleccionar el rango aquí.
- Número 2: argumento opcional. Si ha cubierto todos los datos de la muestra a través del rango, esto se vuelve opcional.
¿Cómo usar la función STDEV.S en Excel?
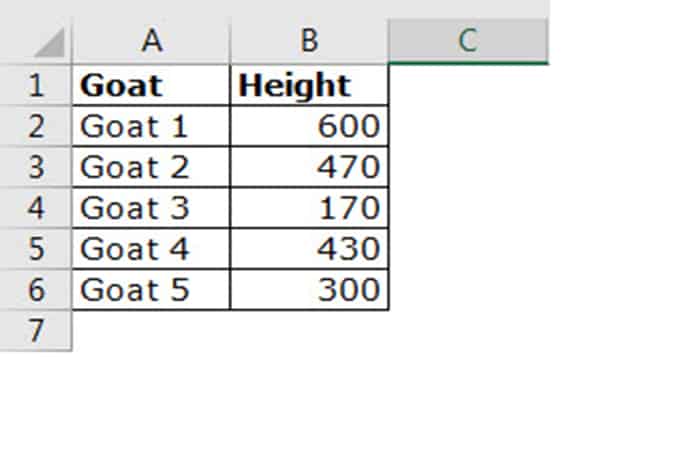
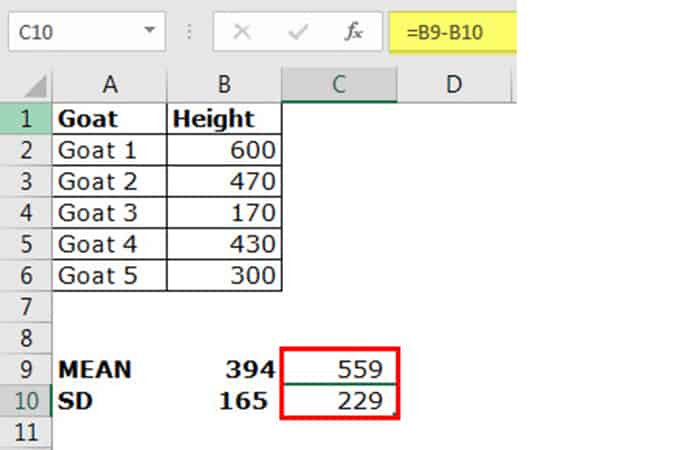
A continuación se muestran los datos de las alturas de la cabra y la altura de cada cabra al nivel del hombro está por debajo.
Nota: las alturas están en milímetros.
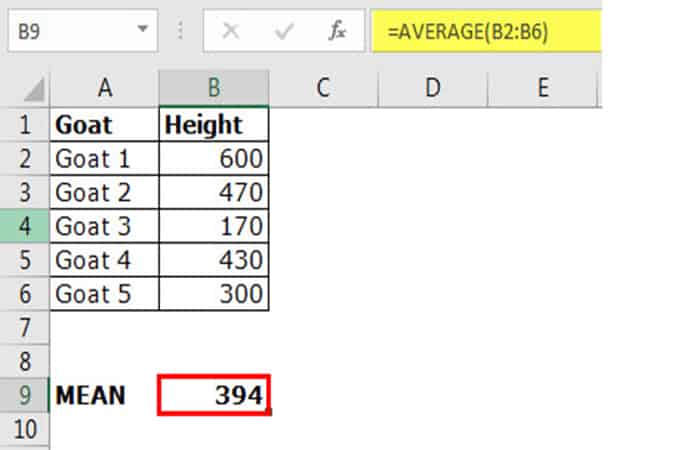
- Paso 1: Calcula el valor medio, es decir, el valor medio.
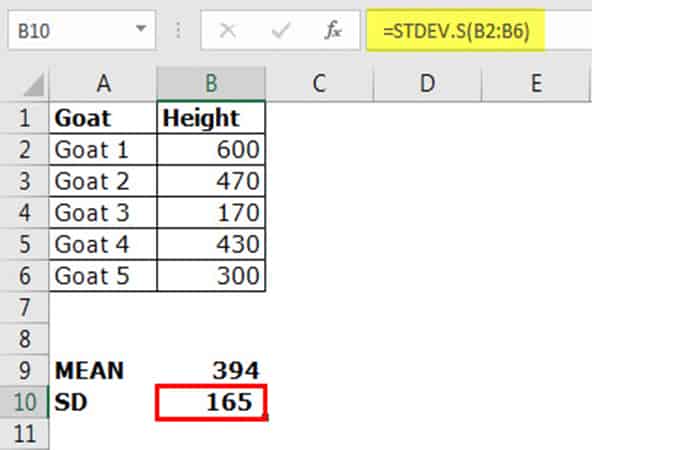
- Paso 2: aplica S en la fórmula de Excel al rango B2: B6.
Entonces, la desviación estándar de la altura de las cabras es 165 (más cercana al milímetro) El valor de 165 milímetros indica que la mayor parte de la altura de la cabra estaría dentro del rango de 229 y 559 milímetros.
Ese es uno de los lados del valor medio, es decir, 394 - 165 = 229 y 394 + 165 = 559.
Nota: Esta es la desviación estándar de la mayoría de las cabras, lo que significa que solo unas pocas están en este rango de altura. Cuando aplicas la fórmula a conjuntos de datos más grandes, verás la mayor diferencia.
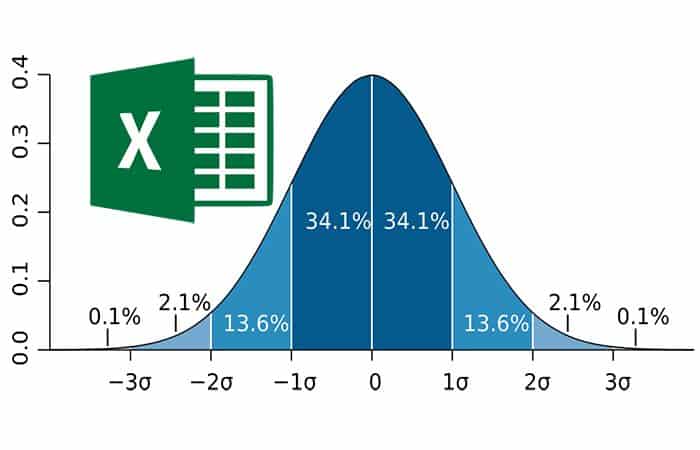
¿Cómo sacar desviación estándar en Excel de manera gráfica?
Como sabemos que la desviación estándar es un cálculo de cómo cambian los valores con la comparación o el respeto de la media o el valor promedio, representamos estos datos en un gráfico, hay dos desviaciones representadas en el gráfico de desviación estándar, una que es positivo a la media que se muestra en el lado derecho del gráfico y otro es negativo a la media que se muestra en el lado izquierdo del gráfico, el gráfico de desviación estándar también se conoce como gráfico de curva de campana en Excel.
Gráfico de desviación estándar de Excel
La desviación estándar es una de las herramientas estadísticas importantes que muestra cómo se distribuyen los datos. Por ejemplo, en el mercado de valores, cómo el precio de las acciones es de naturaleza volátil.
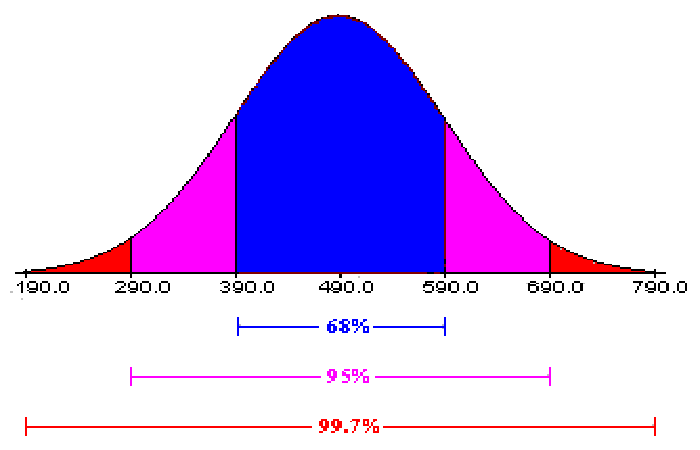
Normalmente, la desviación estándar es la variación a ambos lados del valor medio o medio de los valores de la serie de datos. Podemos trazar la desviación estándar en el gráfico de Excel y ese gráfico se llama "Curva en forma de campana".
Una curva en forma de campana es el gráfico que se usa comúnmente para medir la evaluación del desempeño de los empleados en las empresas. Todas las organizaciones trabajan en la evaluación del desempeño durante un período de tiempo específico, utilizando esta evaluación del desempeño recompensan a los empleados en términos de salario, promociones, etc.
Miden a los empleados en desempeño bajo o sin desempeño, desempeño promedio y desempeño alto. Cuando traza un gráfico en forma de campana, muestra la mayor probabilidad del resultado y la probabilidad del resultado sigue bajando cuando las formas de campana se mueven hacia cualquier lado desde el punto central.
Ejemplo de la "Curva en forma de campana"
Por ejemplo, mire el gráfico de curvas de formas de campana de Excel a continuación.
Supón que estás trabajando en un equipo de 50 miembros y tu calificación es muy similar a la de los otros miembros del equipo, entonces solo unos pocos empleados obtuvieron una calificación más alta, la mayoría obtendrá una calificación promedio y pocos obtendrán una calificación baja. Si obtuviste 8 como calificación y el miembro de tu equipo obtuvo 7 como calificación, no habrá mucha diferencia aquí, ¿verdad?
Para que la comparación justa, la curva en forma de campana se ajuste mejor a la evaluación del empleado y la calificación, recompénsalo en consecuencia.
Todos los empleados de calificación más alta en la curva de campana se colocarán en el lado derecho de la curva de campana, los empleados de calificación baja se colocarán en el lado izquierdo de la curva de campana y los empleados promedio se colocarán en el centro de la curva de campana.
¿Cómo comprender esto?
Para comprender el gráfico de desviación estándar de Excel o la curva en forma de campana, necesitamos dos tipos de cálculos aquí. Uno es MEDIO o PROMEDIO de la serie de datos, y el segundo es la Desviación estándar (SD), que muestra cómo distribuir la serie de datos.
Por ejemplo, si el puntaje promedio de los estudiantes en la clase es 70 y SD es 5, entonces los estudiantes obtuvieron una puntuación dentro de cualquier lado del valor medio, es decir, 70. El primer rango será 65-70 y el segundo rango será 70-75.
¿Cómo hacer desviación estándar en Excel con gráficos?
Para comprender mejor el gráfico de desviación estándar (gráfico) en Excel, consideremos un ejemplo de la vida real con las calificaciones de los estudiantes en un examen.
Hemos tomado datos de muestra de 25 estudiantes y a continuación están los puntajes de estos 25 estudiantes en un examen.
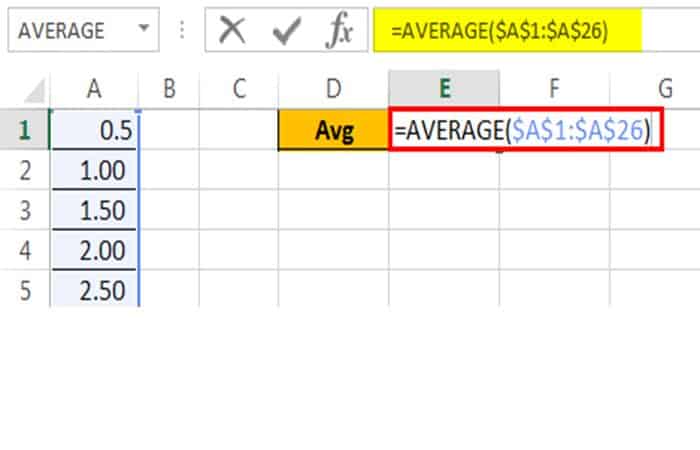
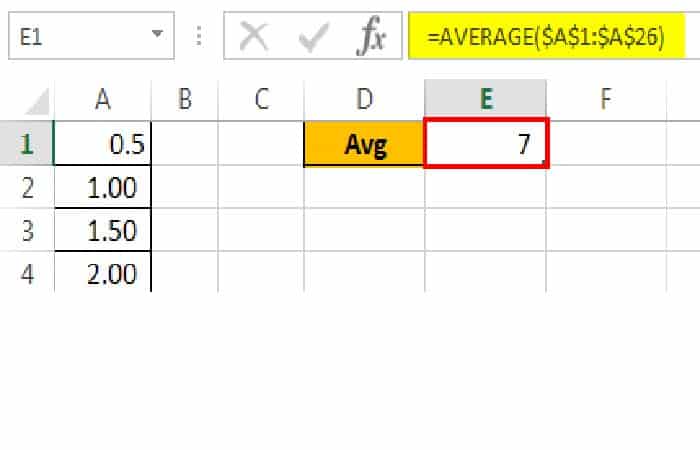
Lo primero que debes hacer es calcular la puntuación PROMEDIO del examen. Aplicar la fórmula promedio.
Obtuvimos el resultado como 7.
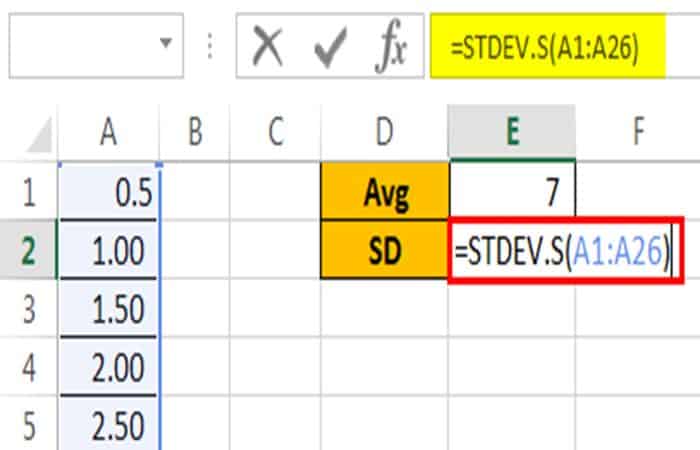
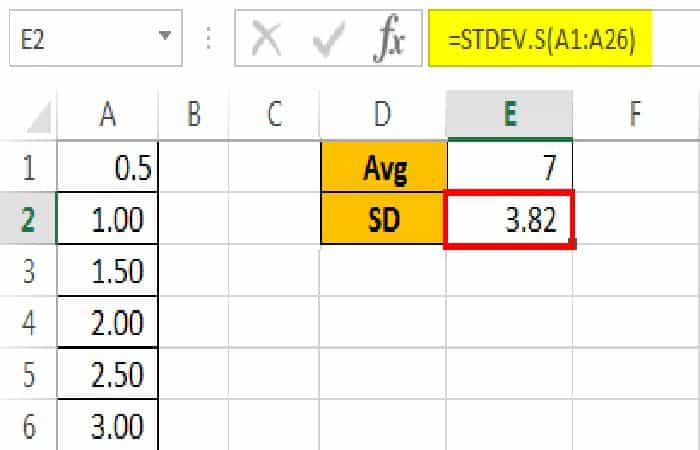
En segundo lugar, calcula la desviación estándar de la serie de datos.
El resultado se muestra a continuación:
Nota: Desde que tomamos datos de muestra, se ha usado STDEV.S, que se usa para series de datos de muestra.
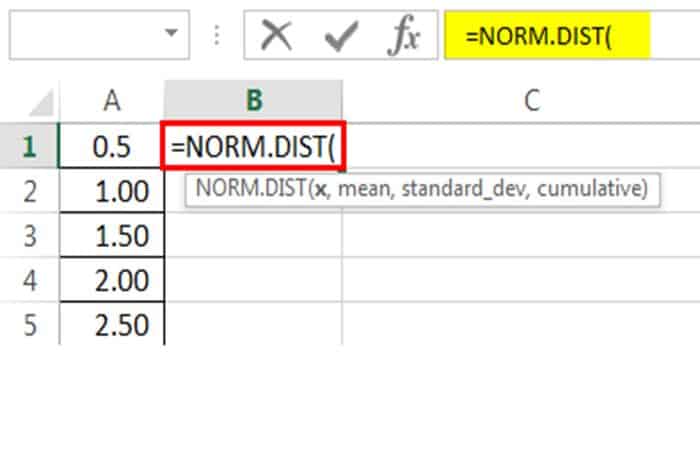
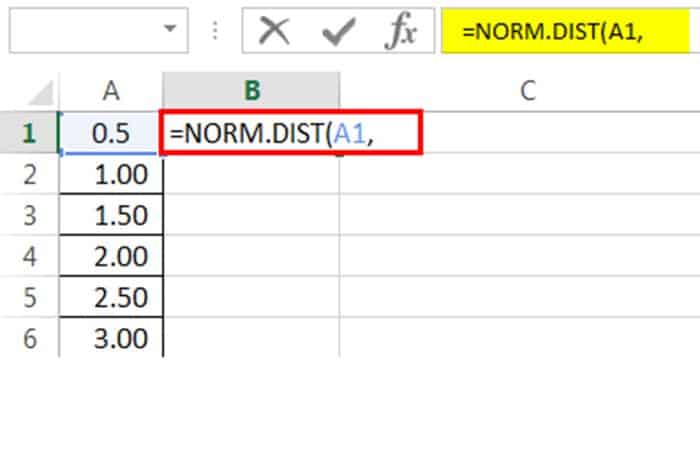
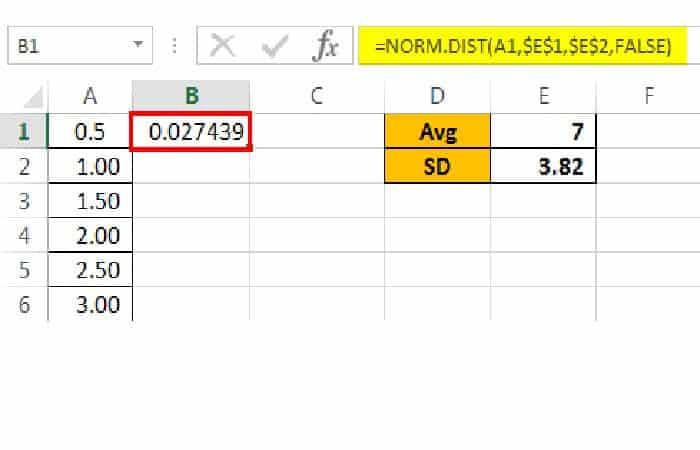
Ahora en la celda B1 ingresa la fórmula de Excel de distribución normal, es decir, NORM.DIST.
X no es más que nuestro punto de datos, así que selecciona la celda A1.
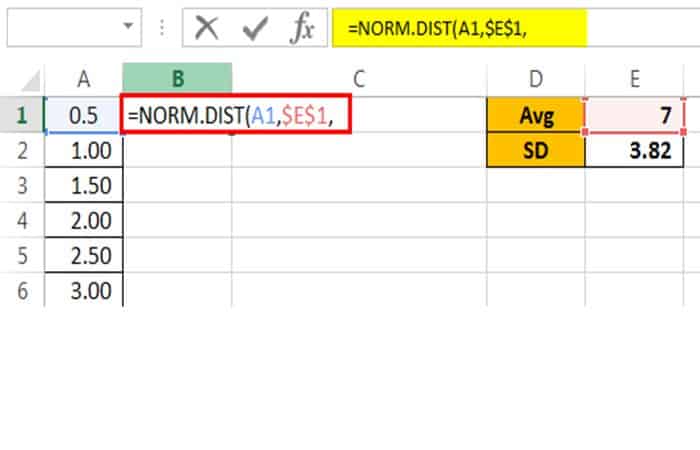
MEAN es el valor promedio que se ha calculado, así que da un enlace a la celda E1 y conviértelo en una referencia absoluta.
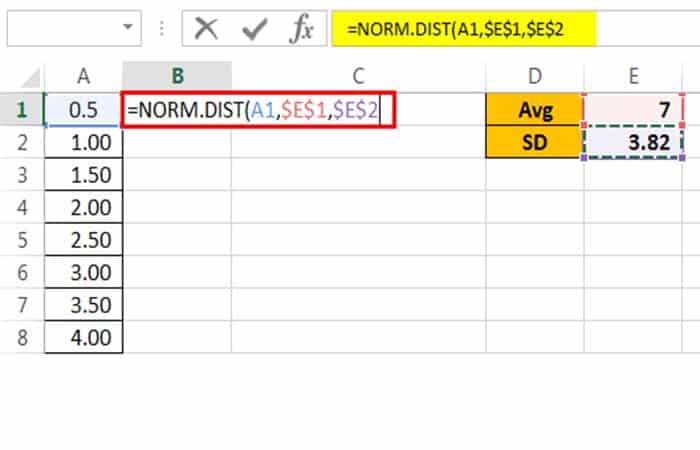
Lo siguiente es SD para proporcionar un enlace a la celda E2 y convertirla en una referencia absoluta de Excel.
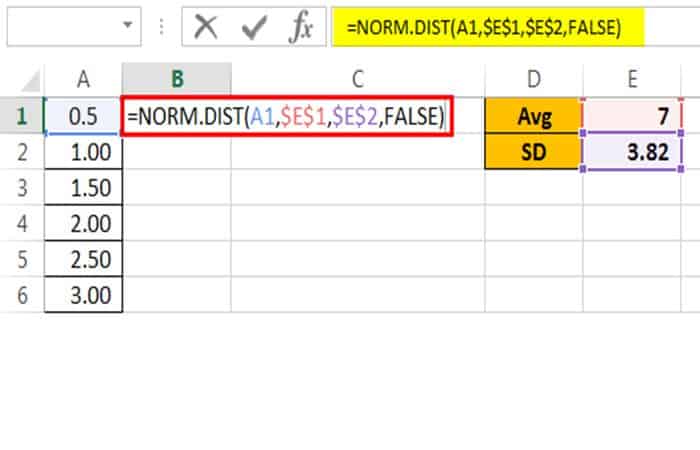
Lo siguiente es acumulativo, seleccione FALSO como argumento.
Ahora mira el resultado.
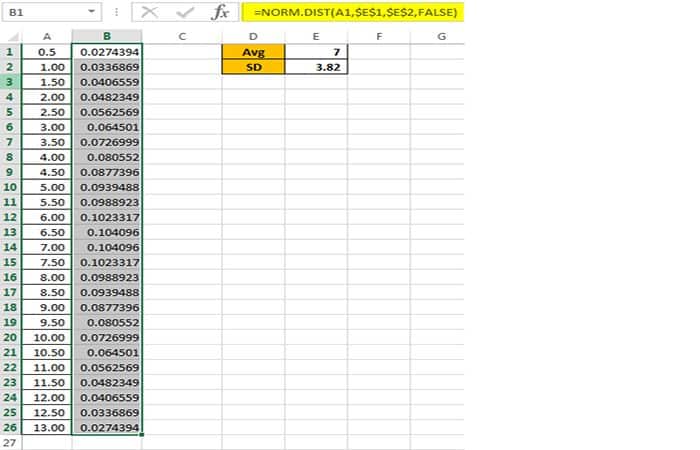
Arrastra la fórmula a otras celdas para tener valores de distribución normales.
Crea un gráfico de Excel de desviación estándar siguiendo los pasos a continuación:
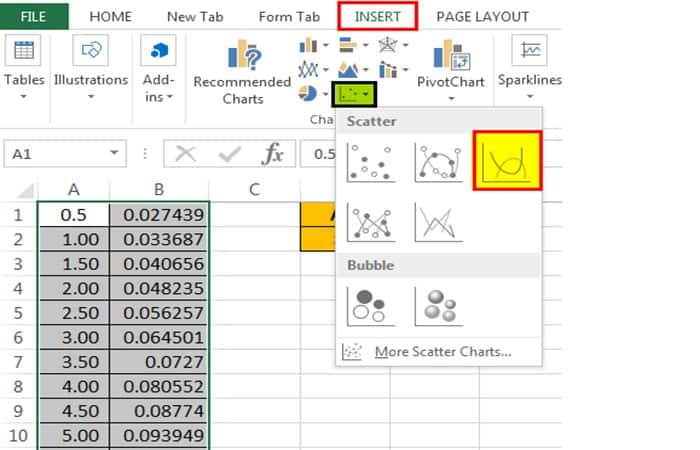
- Paso 1: Selecciona los datos y vaya a la pestaña INSERTAR, luego, en los gráficos, selecciona el gráfico disperso y luego selecciona Gráfico de dispersión más suave.
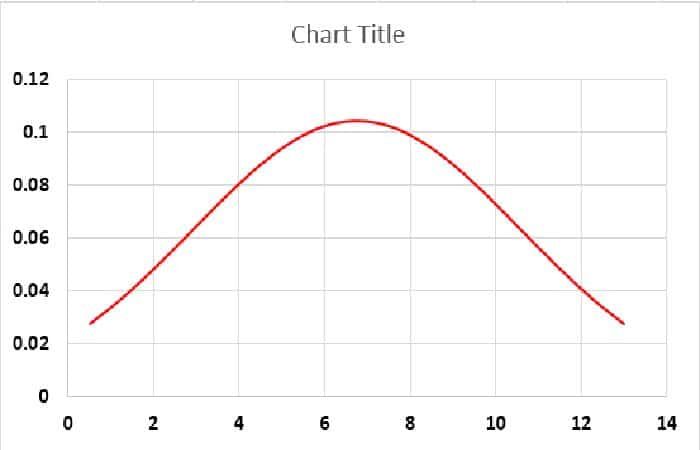
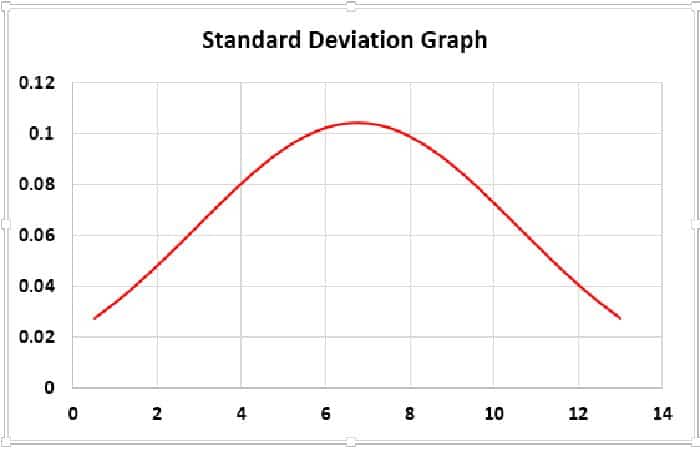
- Paso 2: Ahora tendremos un gráfico como este.
- Paso 3: Si es necesario, puedes cambiar el eje y el título del gráfico.
Este tema está relacionado con: Cómo Hacer Un Organigrama En Excel
Conclusión: Nuestro SD es 3.82, que es un poco más alto, por lo que nuestra curva de campana es más ancha. Si la SD es pequeña, obtendremos una curva de campana delgada.

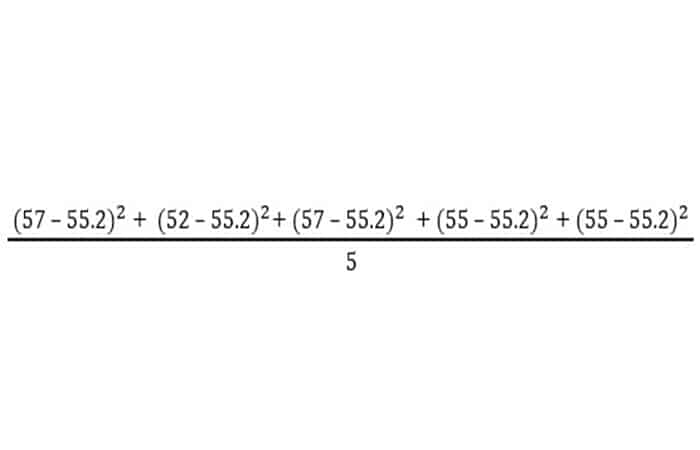
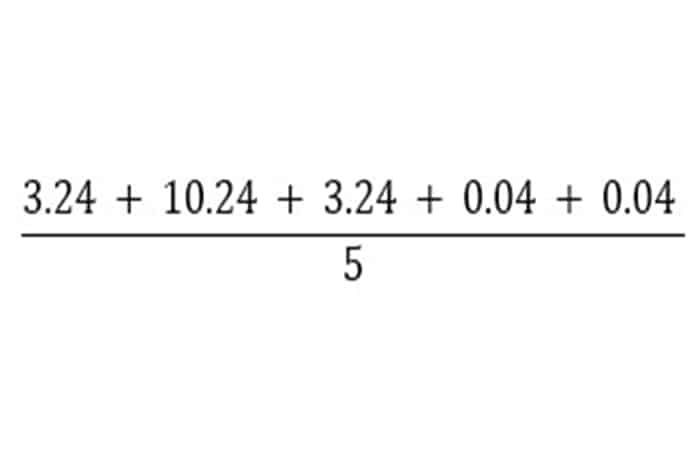
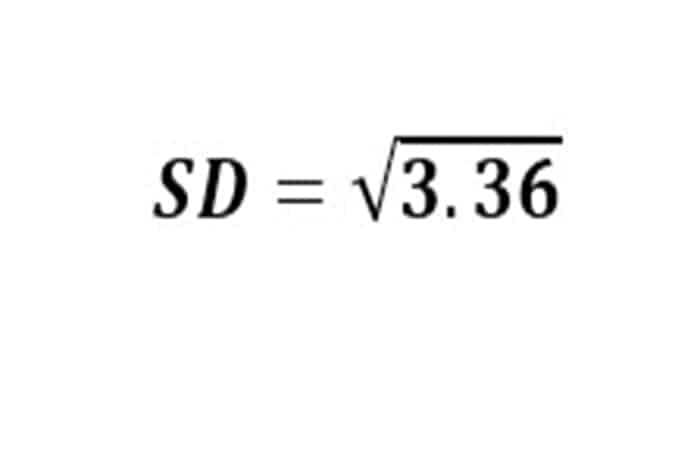

Deja una respuesta